100 天阅读计划,深入剖析程序和计算机 - 增加计算能力
/ / 点击 / 阅读耗时 21 分钟之前部分探讨了有限自动机,这是一种假想的机器,它去掉了真实计算机的复杂性并把其规约成了最简单的形式。我们详细考察了这些机器的行为并了解了它们的用处,而且还发现,非确定性有限自动机虽然有一些奇特的执行方法,但计算能力并不比确定性有限自动机强。那如何增加计算能力呢?
计算能力
我们没法通过为有限自动机增加非确定性和自由移动这种奇特的特性来提高它的计算能力。
这个事实表明,我们已经停留在这些简单机器的计算水平上无法前进了。而且如果不从根本上改变机器的工作方式,将无法脱离这种停滞不前的境地。那么,所有这些机器到底有多强的能力呢?好吧,没有多少能力。它们被限制在非常有限的应用上(只能接受或者拒绝字符序列) ,而且即使在这么小的范围内,仍然很容易碰到机器无法识别的语言。
难题
举个例子,假设要设计一台有限自动机,要求它能读取带有左右括号的字符串,并且只有字符串中的左右括号是平衡的(即每一个右括号都能在字符串中找到与其匹配的左括号) ,它才会接受。
可以设计如下 NFA 来实现:
一次读取一个字符,同时跟踪一个表示当前嵌套级别的数字:读入一个左括号时增加嵌套级别,读入一个右括号时降低嵌套级别。只要嵌套级别到零了,就表示当前读到的这些括号已经都匹配上了(因为嵌套级别增加和减少的数量是一样的) ,并且如果我们试图把嵌套级别降低到小于零的值,那就表明当前的右括号多了(如 ‘())’) ,不管还有什么字符没有读取,字符串里的括号一定已经不平衡了。
缺陷
可是这种设计有一个严重的缺陷:如果括号的嵌套等级超过 3,它就会失败。它没有足够多的状态跟踪 ‘(((())))’ 这样的字符串的嵌套,因此即使括号明显是平衡的它也会拒绝。
我们可以通过临时增加更多的状态来修正此问题。一台拥有 5 个状态的 NFA 可以识别任意嵌套级别小于 5 的平衡字符串,而一台拥有 10 个、100 个或者 1000 个状态的 NFA,可以识别嵌套级别在机器硬限制以内的任意平衡字符串。但是,我们如何设计支持任意嵌套级别、能识别任意平衡字符串的 NFA 呢?结论是设计不出来:一台有限自动机的状态数总是有限的,因此任何机器能支持的嵌套级别也总是有限的,我们只要提供一个比它能处理的嵌套级别多一级的字符串,它就无法处理了。
根本问题是一台有限自动机只有固定的状态集合,因而其存储是有限的,因此没法跟踪任意数量的信息。在平衡字符串问题当中,一台 NFA 很容易递增到设计时限制的某个最大数目,但无法继续计数以适应任何可能大小的输入。
本质上大小固定的任务(比如对字符串 ‘abc’ 进行匹配) ,或者无需跟踪重复次数的任务(比如对正则表达式 ab*c 进行匹配) ,都不受这个问题的影响,但在信息数目不可预知,需要在计算过程中存储并在之后重用的场景下,这个问题会让有限自动机无能为力。
增加计算能力
为了解决存储问题,我们可以使用专门的原始空间扩展有限状态自动机,它负责在计算过程中存储数据。除状态提供的有限内部存储之外,这个空间给了机器一种外部存储(external memory) 。就像我们将会发现的那样,拥有外部存储对于一台机器的计算能力关系重大。
为有限自动机增加存储的简单方式就是让它可以访问栈,这是一个后进先出的数据结构,可以把字符推入和弹出。栈是简单而且有限制的数据结构——在任意时间都只有顶端的字符可以访问。为了查明栈下面位置的数据,我们只能丢弃顶层的字符,而一旦向栈内推入一串字符,我们就只能按相反的顺序把它们弹出——但它确实可以很好地解决有限存储的问题。对于栈的大小并没有内在的限制,因此原则上它可以根据需要存储数据。
自带栈的有限状态机叫作下推自动机(PushDown Automaton,PDA) ,如果这台机器的规则是确定性的,我们就叫它确定性下推自动机(Deterministic PushDown Automaton,DPDA)。
问题解决方案 - 确定性下推自动机 PDA
能对栈进行访问带来了新的可能性,例如,很容易设计一台 DPDA 来识别括号组成的平衡字符串。
- 给机器两个状态:1 和 2,状态 1 作为接受状态。
- 状态 1 作为机器的起始状态,此时栈为空。
- 如果处于状态 1 并且读入一个左括号,就把某个字符——我们使用 b 表示“括号”——入栈,并转移到状态 2。
- 如果处于状态 2 并且读入一个左括号,就把字符 b 入栈。
- 如果处于状态 2 并且读入一个右括号,就把字符 b 从栈中弹出。
- 如果处于状态 2 且栈为空,就转移回状态 1。

非确定性下推自动机 NPDA
尽管处理平衡括号问题的机器确实需要栈来完成工作,但它其实只是将栈作为一个计数器,并且它的规则只区分“栈为空”和“栈不为空” 。更复杂的 DPDA 将会把一种以上的符号推入栈中,并在执行计算时使用这些信息。一个简单的例子是一台机器,它能识别包含相等数目的两种字符的字符串,比如 a 和 b。
DPDA 没有利用栈的全部优点。为了真正开发出栈的潜能,我们需要一个更难的问题强迫我们存储结构化信息。经典的例子是识别回文字符串:随着一个字符一个字符地读取输入字符串,我们需要记住所看到的数据;一旦字符串读取过了一半,就要检查内存以确定之前看到的字符是否为当前呈现字符的逆序。下面这个 DPDA 能够识别一个回文字符串,这个字符串由字符 a 和 b 组成,并且在中间的位置有一个字符 m(表示中间位置) :

这台机器从状态 1 开始,不断从输入读取 a 和 b,然后把它们推入栈中。它读到 m 的时候,会转移到状态 2,在那里一直读取输入字符同时尝试把每一个字符都弹出栈。如果字符串后半部分的每一个字符都与栈中弹出的内容匹配,机器就停留在状态 2 并最终碰到栈底的 $,此时转移到状态 3 并接受这个输入字符串。处于状态 2 的时候,如果读入的任何字符与栈顶的字符不匹配,那就没有规则可以遵守,因此它将进入阻塞状态并拒绝这个字符串。
没有确定性约束的下推自动机叫作非确定性下推自动机(nondeterministic pushdown automaton) 。下面是一台能识别由偶数个字母组成的回文字符串的非确定性下推自动机:
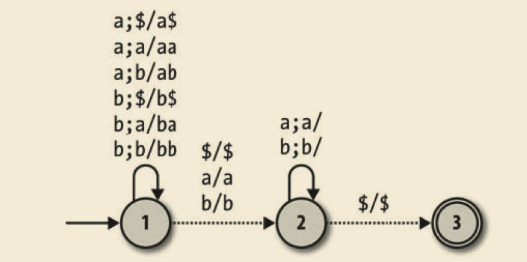
使用下推自动机进行分析
下推自动机有一个重要的实际应用:它们能用来解析编程语言。传统的方式是把解析过程分成两个独立的阶段:
词法分析
读取一个原始字符串然后把它转换成一个单词 token 序列。每一个单词 token 代表程序语法的一个组成部分,例如“变量名” 、 “左括号”或者“while 关键字” 。词法分析器使用称为词法的规则集合来决定什么样的字符应该产生什么样的单词。这个阶段处理杂乱的字符级别的细节,比如变量命名规则、注释和空格,它为下一阶段的处理准备好清楚的单词序列。语法分析
读入一个单词序列并根据正在分析的语言语法判断它们是否代表一个有效的程序。如果程序有效,那么语法解析器会生成一些关于程序结构的附加信息(如一个解析树)。
词法分析
词法分析阶段通常相当直接。这可以通过正则表达式实现(因而也就是通过一台 NFA 实现) ,因为它把字符序列与一些规则简单匹配以判断那些字符是否为关键字、变量名、运算符或者其他什么符号。
语法分析
使用下推自动机是可以识别单词的有效序列。
分析的过程依赖于非确定性,但在实际程序中,最好能避免非确定性,因为一个确定性的 PDA 模拟起来要比非确定性的快得多而且容易得多。幸运的是,在每个阶段几乎都可以使用输入单词本身决定该应用哪个符号规则,这样就可能把非确定性去掉——这个技术叫作递推(lookahead)——但这让从 CFG 到 PDA 的转换更为复杂。
在实践中,我们可以让 PDA 模拟记录它到达接受状态过程中的规则序列,以此来创建结构化表示,这个规则序列提供了构建一个分析树所需的足够信息。
计算能力
我们见到了两个新的计算能力的级别:DPDA 比 DFA 和 NFA 更强大,而NPDA 要比 DPDA 更强大。能访问栈之后,看起来下推自动机比有限自动机要强大和复杂一些。
拥有栈的主要结果就是能识别某些有限自动机不能识别的语言了,如回文和平衡括号字符串。栈提供的无限存储使 PDA 能在计算中记住任意数量的信息并在随后再次使用它。
PDA 能识别回文,但它不能识别 ‘abab’ 和 ‘baaabaaa’ 这样“双倍”的字符串,因为一旦信息被推入到栈中,就只能以相反的顺序处理了。
如果我们抛开识别字符串的特定问题,而把这些机器看成通用目的的计算机,就可以看到DFA、NFA 和 PDA 还远远不够有用。首先,它们都没有像样的输出机制:它们通过进入接受状态表达成功,但不能输出哪怕一个字符(更不用说由字符组成的字符串了)来表示详细的结果。无法将信息发送回世界意味着它们连把两个数相加这样的简单算法都实现不了。而像有限自动机一样,PDA 有一个固定的程序;没有明显的方法构建出一台 PDA 能以某种方式从输入读取一个程序然后运行。
所有这些缺点意味着我们需要一个更好的计算模型,去真正地研究计算机能干什么。
