100 天阅读计划,深入剖析程序和计算机 - 非确定性有限自动机(NFA)
/ / 点击 / 阅读耗时 18 分钟NFA 以及正则表达式的原理。
非确定性
假设我们想要一台有限自动机,它能接受由 a 和 b 组成的第三个字符是 b 的任意字符串。此时很容易想出一个合适的 DFA 设计:
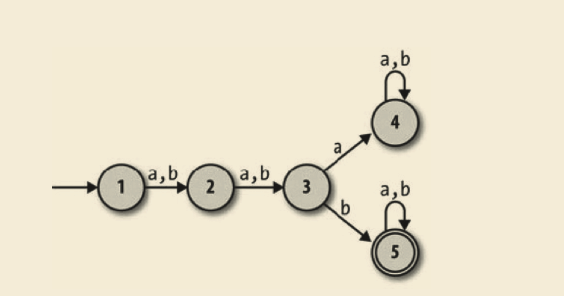
如果想要一台机器能接受倒数第三个字符是 b 的字符串,怎么办呢?那将如何工作呢?似乎更加困难:上面的 DFA 能保证在读第三个字符的时候处于状态 3,但是一台机器无法预先知道什么时候能读到倒数第三个字符,因为在结束读取之前它不知道这个字符串有多长。甚至这样的一台 DFA 是否可能存在都不一定能立刻清楚。
但是,如果我们放松确定性的限制,并且允许规则手册对于一个状态和输入包含多条规则(或者根本没有规则) ,那么就可以设计一台能完成任务的机器:
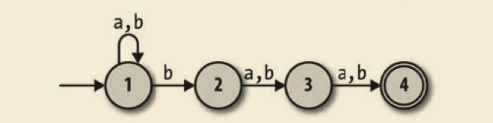
这是一台非确定性有限自动机(NFA) ,对每一个输入序列不再只有一条执行路径。处于状态 1 并且读入 b 的时候,它可能会按照一条规则仍保持在状态 1,但也可能会按照另一条规则进入状态 2。反过来,一旦进入状态 4,它找不到任何规则可以遵守,因此没法再继续读取输入。一台 DFA 的下一状态总是完全由它的当前状态和输入决定,但是一台NFA 在向下一个状态转移时会有多种可能性,而且有时候根本无法转移。
如果一台 DFA 读取一个字符串然后完全按照规则执行,并且最终终止于一个接受状态,那它就能接受这个字符串。那么对于一台 NFA 来说,什么才能表示一台 NFA 接受或者拒绝一个字符串呢?很自然的回答是,如果存在某条路径能让 NFA 按照它的某些规则执行并终止于一个接受状态,那它就能接受这个字符串 ; 这就是说,即使不是必然的,只要终止于一个接受状态是可能的就可以。
例如,这台 NFA 接受字符串 ‘baa’,因为从状态 1 开始,有一条路径可以让这台机器读取一个 b 转移到状态 2,再读取一个 a 转移到状态 3,最后读一个 a 终止于状态 4,这是一个接受态。它还接受字符串 ‘bbbbb’,因为 NFA 可以在读取前两个 b 的时候,按照另一条规则执行并停留在状态 1,然后在读第三个 b 的时候使用规则转移到状态 2,再读取字符串的其他部分,并向以前那样终止于状态 4。
另一方面,没有读取 ‘abb’ 并终止于状态 4 的方法(取决于遵照的不同规则,它最终只能终止于状态 1、2 或者 3) ,因此这台 NFA 不接受 ‘abb’。’bbabb’ 也不行,它最多只能到达状态 3:如果读入第一个 b 的时候直接转移到状态 2,它将很快终止于状态 4,这样留下两个字符没有处理但是已经没有规则可用了。
能被一台特定机器接受的字符串集合称为一种语言:我们说这台机器识别了这种语言。不是所有的语言都有一台 DFA 或者 NFA 能识别它们(详见第 4 章) ,但那些能被有限自动机识别的语言称为正则语言(regular language) 。
模拟
在确定性计算机上模拟一台 NFA,关键是找到一种方法探索出这台机器所有可能的执行。
这种暴力方法把所有的可能全都摆出来,以此避免了只模拟一种可能执行时所需要的“幽灵般”的预见性。一台 NFA 读到一个字符的时候,它下一步转移到什么状态只会有有限数目的可能性,因此我们模拟非确定性时可以尝试遍历所有可能,然后看它们中哪个最终到达一个接受状态。
尝试遍历所有可能时可以采用递归的方式:每当所模拟的 NFA 读取一个字符并且有多个可用的规则时,遵照其中的一条规则,然后尝试读取输入的后续部分;如果这没有让机器到达一个可接受状态,就回退到早期状态,把输入也倒回早期的位置,然后按照另一个不同的规则再次尝试;如此重复,直到某次选择的规则让机器到达一个接受状态,或者所有可能的选择进行遍历的结果都不成功为止。
还有一个策略是采用并行的方式模拟所有可能:每当机器有超过一条规则可以遵守时就创建新线程,并把需要模拟的 NFA 复制过去以便复制的每一份都能尝试一条新规则,然后观察它的结果。所有这些线程都能同时执行,每个都从它自己的输入字符串副本中读取。
如果任何一个线程让机器读取了整个字符串,并且停止于一个接受状态,那么可以说这个字符串已经被接受了。
自由移动
很容易设计一台 DFA,能接受长度是 2 的倍数的、由字符 a 组成的字符串(’aa’、’aaaa’……) :
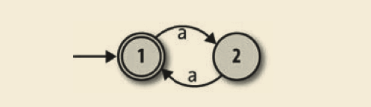
但是如何设计一台机器,让它能接受长度是 2 或 3 的倍数的字符串呢?我们知道非确定性让一台机器可以走多于一条的执行路径,因此或许可以设计一台 NFA,它有一条“2 的倍数”的路径和一条“3 的倍数”的路径。一个初步的尝试可能看起来像这个样子:
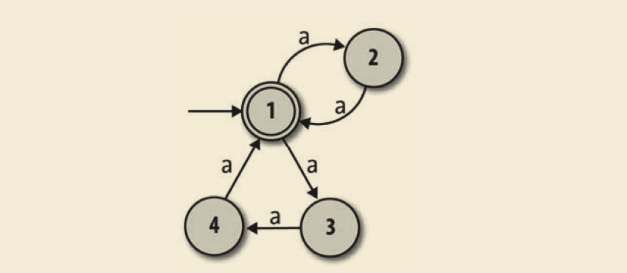
这台 NFA 的思想是,在状态 1 和状态 2 之间移动以接受像 ‘aa’ 和 ‘aaaa’ 这样的字符串,在状态 1、状态 3 和状态 4 之间移动以接受像 ‘aaa’ 和 ‘aaaaaaaaa’ 这样的字符串。这工作得很好,但问题是这台机器还会接受字符串 ‘aaaaa’,因为它可以从状态 1 转移到状态 2 然后读完前两个字符的时候回到状态 1,再在状态 3 和状态 4 之间转移,之后在读完接下来的三个字符之后回到状态 1,终止于一个接受状态,即使这个字符串的长度不是 2 或者3 的倍数。
这次,一台 NFA 是否能完成这个工作还不是很明显,但是我们可以引入一个叫作自由移动的机器特性来解决此问题。这些规则让机器无需读取任何输入就能自发遵照执行,并且它们在这儿提供帮助是因为能让 NFA 在两组状态之间做一个初步选择:
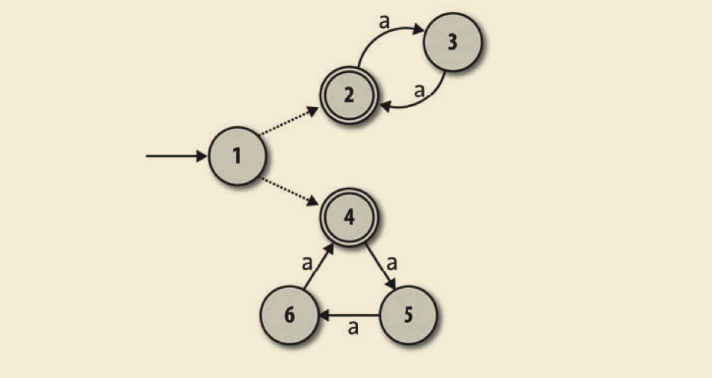
自由移动表示成从状态 1 到状态 2 和状态 4 的无标记虚线箭头。机器仍然接受字符串’aaaa’,它会先自发地转移到状态 2,然后随着读取输入在状态 2 和状态 3 之间转移。类似地,如果它开始先自由移动到状态 4 也能接受 ‘aaaaaaaaa’。但是现在它没法接受字符串 ‘aaaaa’ 了:不管做任何可能的执行,它都一定要从到状态 2 或者状态 4 的转移开始,而且一旦选择了其中一条路径转移之后,就没法退回来了。一旦处于状态 2,就只能接受一个长度是 2 的倍数的字符串,同样一旦处于状态 4,就只能接受长度是 3 的倍数的字 符串。
正则表达式
非确定性和自由移动增强了有限自动机的表达能力。
有限自动机完全适合这个工作。就像我们即将看到的,把任何正则表达式转成一个等价的 NFA 是可能的——每一个与正则表达式匹配的字符串都能被这台 NFA 接受,反过来也一样——把字符串输入给一台模拟的 NFA 看它是否能被接受,从而判断字符串是否与正则表达式匹配。用第 2 章的话说,我们可以把这个看成是为正则表达式提供了一种指称语义:我们不一定知道如何直接执行一个正则表达式,但是可以展示如何把它表示成一台NFA,并且因为有了 NFA 的操作语义( “通过读取字符然后执行规则改变状态” ) ,所以可以执行这个指称(denotation)实现同样的结果。
等价性
把任何非确定性有限自动机转成接受完全相同字符串的确定性自动机是可能的。
非确定性和自由移动只是一台 DFA 已经能做的工作的再包装,就像编程语言里中的语法糖一样,它们不是让我们超越确定性约束的新能力。
理论上说,为一台简单的机器增加更多的特性却没有为它根本上增加更多的能力非常有趣,但实际上这是很有用的,因为一台 DFA 比一台 NFA 更容易模拟:只有一个当前状态要跟踪,并且一台 DFA 用硬件或者机器代码实现起来足够简单,可以使用程序存储位置作为状态,用条件分支作为规则。这意味着一个正则表达式的实现可以把一个模式先转换成一台 NFA 然后再转换成一台 DFA,得到一台能被快速高效模拟的非常简单的机器。
