100 天阅读计划,深入剖析程序和计算机 - 计算的通用性
/ / 点击 / 阅读耗时 17 分钟通用图灵机的存在是极其有意义的。尽管任何一台个体的图灵机都有一个硬编码的规则手册,但是通用图灵机证明了设计这样一个装置的可能性,这个装置可以通过从纸带读取指令来完成任何任务。这些指令实际上是控制机器硬件运行的软件,就像控制我们每天都在使用的通用可编程计算机的软件一样1。有限和下推自动机有点过于简单,不能支持这种全面的可编程性,但是图灵机具有解决这个问题的足够的复杂性。
lambda 演算通用性
lambda 演算是一种可用的编程语言,但还没有探讨它是否与图灵机一样强大。事实上,lambda 演算一定至少有那么强大,因为它能够模拟包括通用图灵机(当然包括)在内的任何图灵机。
通用系统的真正好处是它能被编程以执行不同的任务,而不是总要硬编码来。
特别地,通用系统能被编程来模拟任何其他的通用系统;通用图灵机能计算 lambda 演算表达式的值,而 lambda 演算解释器也能模拟图灵机。
SKI 组合子
就像 lambda 演算一样,SKI 组合子演算是一个处理表达式语法的规则系统。尽管 lambda 演算已经很简单了,但仍然还有三种表达式:变量、函数和调用。
SKI 演算更简单,它只有两种表达式:调用和字母符号,规则也更简单。它所有的能力都源于三个特别的符号 S、K 和 I(叫作组合子) ,它们每一个都有自己的归约规则:
- 规约成 a[c][b[c]],其中 a、b 和 c 可以是任意的 SKI 演算表达式;
- K[a][b]规约成 a
- I[a] 规约成 a
SKI 演算用三个简单的规则就产生了出人意料的复杂行为。事实上,复杂到被证明是通用的了。我们可以证明 SKI 表达式的通用性,方法是展示如何把任意的 lambda 演算表达式转换成做同样事情的一个 SKI 表达式,这实际上也是使用 SKI 演算给了 lambda 演算一个指称语义。我们已经知道 lambda 演算是通用的,因此如果 SKI 能完全模拟它,就能得出SKI 演算也是通用的结论。
约塔(Iota)
希腊字母约塔(ɩ)是可以添加到 SKI 演算里的另一个组合子。下面是它的规约规则:ɩ[α] 可以规约成 α[S][K]。
Chris Barker 提交了一种叫作 Iota(http://semarch.linguistics.fas.nyu.edu/barker/Iota/)的语言,它的程序只使用 ɩ 组合子。尽管只有一个组合子,Iota 仍然是一种通用语言,因为任何 SKI 演算表达式都可以转成它,而我们已经看到 SKI 演算是通用的。
可以通过应用这些替换规则把 SKI 表达式转成 Iota:
- 用 ɩ[ɩ[ɩ[ɩ[ɩ]]]] 替换 S
- 用 ɩ[ɩ[ɩ[ɩ]]] 替换 K
- 用 ɩ[ɩ] 替换 I
标签系统
标签系统(tag system)是一个类似简化版图灵机的计算模型:标签系统不是在一条纸带上来回移动纸带头,而是反复在一个字符串的末尾增加新的字符并在开头处移除字符。在某方面,标签系统的字符串像是图灵机的纸带,但标签系统被限定在只能在字符串的两头操作,而且它只能朝着末尾“移动” 。
标签系统的描述包括两部分:首先,一个规则集合,其中每一条规则定义当特定的字符出现在字符串的开头时,要给这个字符串添加的一些字符(例如“字符串的开头是字符 a 时,添加字符 bcd” ) ;其次,一个叫作删除数的数字,它定义了按照一个规则执行之后有多少字符要从字符串的开头删除。
标签系统只能直接在字符串上操作,但我们也可以让它们对其他类型的值(例如数字)执行复杂的操作,只要用合适的方式把那些值编码成字符串就行。对数字编码的一种可能方式是:把数字 n 表示成字符串 aa 后跟重复 n 次的字符串 bb。例如,把数字 3 表示成字符串 aabbbbbb。
对于标签系统如何模拟图灵机工作的完整说明,请看 Matthew Cook 在 http:// www.complex-systems.com/pdf/15-1-1.pdf 中 2.1 节所做的简洁解释。
标签系统可以模拟任意图灵机的事实,意味着它也是通用的。
循环标签系统
循环标签系统(cyclic tag system)是施加了一些额外限制的更简单的标签系统。
- 循环标签系统的字符串只能包含两个字符:0 和 1
- 循环标签系统的规则只会在当前字符串以 1 开始而不是 0 开始的时候才会应用
- 循环标签系统的删除数总 1
这些约束本身对于支持任何有用的计算来说都过于苛刻了,因此作为补偿循环标签系统有一个额外的特性:循环标签系统的规则手册中的第一条规则是执行开始时的当前规则,并且在计算的每一步之后,规则手册中的下一个规则就成为了当前规则,在到达规则手册结尾的时候又会回到第一个规则。
这种系统被称为“循环的” ,是因为当前规则不断地在规则手册中循环。一个当前规则,再结合上每条规则都只会应用到 1 开头的字符串这一约束,避免了在每一步执行中不得不遍历规则手册查找可用规则的开销。如果首字符是 1,那么就应用当前规则,否则,就没有可用的规则。
循环标签系统极其受限(它们的规则不灵活,只有两个字符,删除数也是最低值) ,但令人吃惊的是,仍然可以使用它们模拟任何标签系统。
循环标签系统也是通用的。
Conway 的生命游戏
1970 年,John Conway 发明了一个叫作生命游戏(Game of Life)的通用系统。 “游戏”要在一个无限多的二维网格里进行,网格的每个小方格可以是生或是死。一个小方格有 8 个邻居:它上面的三个单元,紧挨着它的左右两个单元,以及它下面的三个单元。
生命游戏像有限状态机那样分一系列步骤进行。在每一步,根据由这个单元自身的当前状态和它邻居的状态所触发的规则,每个单元都可能从生转变为死,或者相反。规则很简单:如果一个活着的单元有少于两个(人口稀少)或者多于三个(人口过剩)活着的邻居,它就会死掉,如果一个死的单元恰好有三个活着的邻居它就能复活(繁殖) 。
1982 年,Conway 除了展示如何靠以创造性的方式碰撞“滑翔机”来设计逻辑上的与门(AND) 、或门(OR)和非门(NOT)以执行数字计算之外,还展示了如何使用一连串的“滑翔机”来表示二进制数据。这些结构说明理论上可以用生命游戏模拟一个数字计算机,但 Conway 没有设计出来一台可工作的机器。
2002 年,Paul Chapman 实现了一个特种通用计算机(http://www.igblan.free-online.co.uk/igblan/ ca/) 。而 2010 年,Paul Rendell 构造出了一台通用图灵机(http://rendell-attic.org/gol/utm/) 。
rule 110
rule 110 是另一个细胞自动机,由 Stephen Wolfram 在 1983 年提出。与 Conway 生命游戏里每个单元要么是生的要么是死的类似,rule 110 操作的单元按一维排列而不是二维网格形式。这意味着每个单元只有两个邻居而不是围绕着每个生命游戏单元的 8 个邻居。
2004 年,Matthew Cook 发表了一个对 rule 110 事实上通用的证明。这个证明包含大量的细节(参考 http://www.
complex-systems.com/pdf/15-1-1.pdf 的第 3 节和第 4 节) 。但粗略地讲,它引入了几个不同的 rule 110 模式扮演“滑翔机”的角色,然后通过用一种特定的方式排列那些“滑翔机”来展示如何模拟任意循环标签系统。
这意味着 rule 110 可以运行一个循环标签系统的模拟,而循环标签系统又可以运行一个普通标签系统的模拟,普通标签系统可以运行一个通用图灵机的模拟。这不是完成通用计算的高效方式,但对这样一台简单的细胞自动机来讲仍然是一项令人印象深刻的技术成果。
Wolfram 的 2,3 图灵机
我们要介绍的最后一个简单通用系统甚至比 rule 110 还简单:Wolfram 的 2,3 图灵机。它的名字源于其两个状态和三个字符(a、b 和空格) ,这意味着它只有 6 个规则:
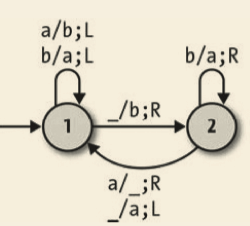
Wolfram 的 2,3 图灵机看起来没有强大到能支持通用计算。2007 年,Wolfram Research 宣布将给予能证明它是通用的人 25 000 美元的奖励。那年下半年,Alex Smith 通过成功的证明拿到了这个奖。就像对 rule 110 一样,这个证明靠的是展示出这种机器可以模拟任何循环标签系统。这个证明还是非常详细的,在 http://www.wolframscience.com/prizes/tm23/ 可以看到全文。
